JSPLib

The jobshop scheduling problem benchmark library

JSPLib is a comprehensive benchmark library for the Job Shop Scheduling Problem (JSP). It serves as a centralized repository for standard instances (ft, la, abz, orb, yn, swv, ta, dmu and tai) and tracks the current State-of-the-Art (SOTA) by maintaining verified Best Known Solutions (BKS).

The data and source code can be found in the Github repository This document is visible as a README.md in the Github folder jobshop or as a webpage. Instances and best known solutions are now available in json or text format

Jobshop instances
Jobshop and variants
JSPLib solutions - The State-Of-The-Art
- Best known solutions
- Publications
Comparison of reference engines

Overview of the jsplib

Jobshop instances (332)

3 instances ft from Fischer and Thompson 1963
40 instances la from Lawrence 1984
5 instances abz from Adams, Balas and Zawack 1988
10 instances orb from Applegate and Cook 1991
4 instances yn from Yamada and Nakano 1992
20 instances swv from Storer, Wu and Vaccari 1992
80 instances ta from Taillard 1993
80 instances dmu from Demirkol, Mehta and Uzsoy 1998
90 instances tai from Da Col and Teppan 2022

Reentrant jobshop instances (24)

12 instances long from Da Col and Teppan 2022
12 instances short from Da Col and Teppan 2022

Classification of the jobshop instances

We use the following engines as reference engines for the benchmark for they are widely considered the strongest engines for scheduling, and to provide a balanced benchmark across different solver technologies

IBM ILOG CP Optimizer : a classic CP-scheduling engine
Google CP-SAT : a lazy clause generation + LP + local search engine
OptalCP : a modern CP-scheduling engine

Instances are divided into

easy : solved to optimality (with proof) in 1 minute by at least 1 reference engine
medium : solved to optimality (with proof) in 1 hour by at least 1 reference engine
hard : solved to optimality (with proof) in > 1h by at least 1 reference engine
closed : allegedly solved to optimality. Most of the time the optimal solution is known because 2 different methods independently found equal upper and lower bounds. The problem moves to hard only when the optimality proof can be reproduced by a reference engine.
open : no proof of optimality

Currently the instances are distributed as follows

ft : 3 easy
la : 39 easy, 1 medium
abz : 2 easy, 2 medium, 1 hard
orb : 10 easy
yn : 4 hard
swv : 7 easy, 7 medium, 3 hard, 3 open
ta : 40 easy, 21 medium, 7 hard, 12 open
dmu : 17 easy, 13 medium, 5 hard, 45 open
tai : 50 easy, 40 open
long : 11 easy, 1 medium
short : 5 easy, 6 medium, 1 open

Similar work

Our work was inspired by the outstanding work of Naderi, Ruiz and Roshanaei Mixed-Integer Programming versus Constraint Programming for shop scheduling problems : New Results and Outlook [NRR2022] which compares CPO, Cplex, Gurobi and OR-tools on a benchmark of 6623 instances over 17 benchmarks with a timeout of 1h. They have made all the raw results available

We borrowed references for existing best known bounds from

The upper bounds available in optimizizer are verified before publication (which we don’t do directly - our verification is the fact that an engine achieves the same value). We encourage you to also visit his site.

We also think https://www.jobshoppuzzle.com/ is a very cool site with interactive visualizations of jobshop heuristics and solutions.

Formats

There are four main formats, standard, DaColTeppan, taillard and json.

The flexible jobshop library preferred format represents precedences explicitly. The jobshop problem being a special case of the flexible jobshop problem, this library may at some point in the future use that same format

Standard format

#n #m
((machine duration ){m}\n){n}

For instance la01 on standard format is

5	
21	0	53	4	95	3	55	2	34
21	3	52	4	16	2	26	1	71
39	4	98	1	42	2	31	0	12
77	0	55	4	79	2	66	3	77
83	3	34	2	64	1	19	4	37
54	2	43	4	79	0	92	3	62
69	4	77	1	87	2	87	0	93
38	0	60	1	41	3	24	4	83
17	1	49	4	25	0	44	2	98
77	3	79	2	43	1	75	0	96

Da Col Teppan format

#n #m
((machine duration )+ -1 -1\n){n}

In the DaColTeppan format

there can be any number of tasks per job
there can be various tasks in a job running on the same machine (reentrance)
the jobs end in a -1 -1

The DaColTeppan format is actually a format for the reentrant jobshop problem which is a generalization of the jobshop, common in some industrial environments like semiconductors

A modified instance of la01 would look like

5	
21	0	53	-1  -1
21	3	52	 4	16	2	26	1	71   4	95	3	55	 2	34 -1 -1
39	4	98	 1	42	2	31	0	12  79	 2	66	3	77  -1 -1
77	0	55	 4  -1 -1
83	-1 -1
54	2	43	4	79	0	92	3	62   3	34	 2	64	 1	19	4	37 -1 -1
69	4	77	1	87	2	87	0	93  41	 3	24	 4	83  -1 -1
38	0	60	1	-1 -1
17	1	49	4	25	0	44	2	98 -1 -1
77	3	79	2	43	1	75	0	96 -1 -1

To be totally conservative, the format should remove the last two -1 -1 and consider the end of line is the separator between jobs. It is not hard to do a parser that accepts both.

Taillard format

The taillard format first lists the machines, then the durations

#n #m
((machine ){m}\n){n}
((duration ){m}\n){n}

For instance la01 in taillard format is

5	
0	4	3	2
3	4	2	1
4	1	2	0
0	4	2	3
3	2	1	4
2	4	0	3
4	1	2	0
0	1	3	4
1	4	0	2
3	2	1	0
53	95	55	34
52	16	26	71
98	42	31	12
55	79	66	77
34	64	19	37
43	79	92	62
77	87	87	93
60	41	24	83
49	25	44	98
79	43	75	96

JSON format

The json format is more verbose but probably easier to use and contains meta-data about the instance that is useful for automating benchmarks

{
  "instance": "la01",
  "family": "la",
  "family_long": "Lawrence",
  "year": "1984",
  "machines": 5,
  "jobs": 10,
  "data": [
  {"job": 0, "operation": 0, "machine": 1, "duration": 21},
  {"job": 0, "operation": 1, "machine": 0, "duration": 53},
  {"job": 0, "operation": 2, "machine": 4, "duration": 95},
  {"job": 0, "operation": 3, "machine": 3, "duration": 55},
  {"job": 0, "operation": 4, "machine": 2, "duration": 34},
  {"job": 1, "operation": 0, "machine": 0, "duration": 21},
  {"job": 1, "operation": 1, "machine": 3, "duration": 52},
  {"job": 1, "operation": 2, "machine": 4, "duration": 16},
  {"job": 1, "operation": 3, "machine": 2, "duration": 26},
  ...
    {"job": 9, "operation": 4, "machine": 0, "duration": 96}
  ]
}

Publications (instances)

The instances come from the following publications

H. Fisher, G.L. Thompson (1963), Probabilistic learning combinations of local job-shop scheduling rules, J.F. Muth, G.L. Thompson (eds.), Industrial Scheduling, Prentice Hall, Englewood Cliffs, New Jersey, 225-251.
Lawrence, S. (1984). Resource constrained project scheduling: An experimental investigation of heuristic scheduling techniques (Supplement). Graduate School of Industrial Administration, Carnegie-Mellon University.
Adams, J., Balas, E., & Zawack, D. (1988). The shifting bottleneck procedure for job shop scheduling. Management science, 34(3), 391-401.
Applagate, D., & Cook, W. (1991). A computational study of the job-shop scheduling instance. ORSA J. Comput, 3, 49-51.
Storer, R. H., Wu, S. D., & Vaccari, R. (1992). New search spaces for sequencing instances with application to job shop 38 (1992) 1495–1509 Manage. Sci, 38, 1495-1509.
T. Yamada, R. Nakano (1992), A genetic algorithm applicable to large-scale job-shop instances, R. Manner, B. Manderick (eds.),Parallel instance solving from nature 2, North-Holland, Amsterdam, 281-290
Taillard, E. (1993). Benchmarks for basic scheduling problems. european journal of operational research, 64(2), 278-285.
Demirkol, E., Mehta, S., & Uzsoy, R. (1998). Benchmarks for shop scheduling problems. European Journal of Operational Research, 109(1), 137-141.
Da Col, G., & Teppan, E. C. (2022). Industrial-size job shop scheduling with constraint programming. Operations Research Perspectives, 9, 100249.

Jobshop variants

Many variants of the jobshop problem can be solved with the same data or simple addition of parameters

Jobshop

The classical jobshop problem has 2 constraints

intrajob precedences

\[\forall j \in \mathrm{jobs}, \forall r \in \mathrm{ranks} \quad \mathrm{start}_j^r + \mathrm{Duration}_j^r \leq \mathrm{start}_j^{r+1}\]

no overlap per machine

\[\forall m \in \mathrm{machines}, \forall j_1,j_2 \in \mathrm{jobs} \quad \left( \mathrm{start}\_{j_1}^m + \mathrm{Duration}\_{j_1}^m \leq \mathrm{start}\_{j_2}^m \right) \vee \left( \mathrm{start}\_{j_2}^m + \mathrm{Duration}\_{j_2}^m \leq \mathrm{start}\_{j_1}^m \right )\]

For commodity the later constraint can be written

\[\forall m \in \mathrm{machines} \quad \mathrm{noOverlap} \ \lbrace \ [ \mathrm{start}_j^m \dots \ \mathrm{start}_j^m + \mathrm{Duration}_j^m ] \mid j \in \mathrm{jobs} \ \rbrace\]

No buffer jobshop (blocking jobshop)

In the classic jobshop there is implicitly a buffer area in front of each machine where tasks can wait to be processed. In the non-buffer jobshop, also called blocking jobshop this area doesn’t exist, as a result a job (j,r)processed on machine m blocks this machine until (j,r+1) starts being processed on the next machine.

From this problem we introduce a new variable $\mathrm{end}_j^m$

the tasks are variable length with a minimum length of $\mathrm{Duration}_j^m$

\[\forall j \in \mathrm{jobs}, \forall r \in \mathrm{machines} \quad \mathrm{start}_j^m + \mathrm{Duration}_j^m \leq \mathrm{end}_j^m\]

for each job, the task of rank $r+1$ starts as soon as the task of rank $r$ ends

\[\forall j \in \mathrm{jobs}, \forall r \in \mathrm{ranks} \quad \mathrm{end}_j^r = \mathrm{start}_j^{r+1}\]

no overlap per machine

\[\forall m \in \mathrm{machines}, \forall j_1,j_2 \in \mathrm{jobs}\quad \left( \mathrm{end}\_{j_1}^m \leq \mathrm{start}\_{j_2}^m \right) \vee \left( \mathrm{end}\_{j_2}^m \leq \mathrm{start}\_{j_1}^m \right )\]

\[\forall m \in \mathrm{machines} \quad \mathrm{noOverlap} \ \lbrace \ [ \mathrm{start}_j^m \dots \ \mathrm{end}_j^m ] \mid j \in \mathrm{jobs} \ \rbrace\]

The extra variables $\mathrm{end}$ can be pre-processed out of the equations

No-wait jobshop

In the no-wait jobshop variant, once the processing of a job has started, it has to go through all machines without interruption.

The equations are reminiscent of the blocking jobshop but without the variable length activities

for each job, the task of rank $r+1$ starts as soon as the task of rank $r$ ends

\[\forall j \in \mathrm{jobs}, \forall r \in \mathrm{ranks} \quad \mathrm{end}_j^r = \mathrm{start}_j^{r+1}\]

no overlap per machine

\[\forall m \in \mathrm{machines} \quad \mathrm{noOverlap} \ \lbrace \ [ \mathrm{start}_j^m \dots \ \mathrm{end}_j^m ] \mid j \in \mathrm{jobs} \ \rbrace\]

Cumulative jobshop

In the cumulative jobshop, the capacity of the capacity of the machines is not unitary anymore. In other words there is a limit $C_m$ on the number of tasks that can be simultaneously processed by machine $m$

The constraints of the problem are

intrajob precedences

\[\forall j \in \mathrm{jobs}, \forall r \in \mathrm{ranks} \quad \mathrm{start}_j^r + \mathrm{Duration}_j^r \leq \mathrm{start}_j^{r+1}\]

capacity per machine

\[\forall m \in \mathrm{machines}, \forall t \in \mathrm{time} \quad \sum_j \left( \mathrm{start}^m_j \leq t \lt \mathrm{start}^m_j + \mathrm{Duration}^m_j \right) \leq C_m\]

It is advisable to avoid having an unlimited number of equations, in this case because of the explicit dependency on time, even if it just for notation. We therefore introduce the functional notation for cumulative constraints

\[\forall m \in \mathrm{machines}\quad \mathrm{cumul}_m(t) = \sum_j \mathrm{step}(\mathrm{start}_j^m) - \mathrm{step}(\mathrm{start}_j^m + \mathrm{Duration}_j^m)\]

Here $\mathrm{step}(t)$ is the function that has value 1 at time $t$ and 0 otherwise, as a result $\mathrm{cumul}$ is a function of time. Each configuration of $\mathrm{start}_j^m$ values defines a different cumulative function.

The constraints of the problem become

intrajob precedences

\[\forall j \in \mathrm{jobs}, \forall r \in \mathrm{ranks} \quad \mathrm{start}_j^r + \mathrm{Duration}_j^r \leq \mathrm{start}_j^{r+1}\]

capacity per machine

\[\forall m \in \mathrm{machines}\quad \sum_j \mathrm{step}(\mathrm{start}_j^m) - \mathrm{step}(\mathrm{start}_j^m + \mathrm{Duration}_j^m) \leq C_m\]

Jobshop with operators - workers

In the jobshop with operators, workers have to be assigned to the machines while the tasks are being performed.

when the operator assignment can be interrupted (preemptive operators) the problem becomes a jobshop with maximum number of simultaneous jobs.
when the operator assignment cannot be interrupted (non-preemptive operators) the operators need to be assigned to jobs individually and they cannot be assigned to simultaneous jobs

Jobshop with preemptive operators

The constraints of the problem become

intrajob precedences

\[\forall j \in \mathrm{jobs}, \forall r \in \mathrm{ranks} \quad \mathrm{start}_j^r + \mathrm{Duration}_j^r \leq \mathrm{start}_j^{r+1}\]

no overlap per machine

\[\forall m \in \mathrm{machines} \quad \mathrm{noOverlap} \ \lbrace \ [ \mathrm{start}_j^m \dots \ \mathrm{start}_j^m + \mathrm{Duration}_j^m ] \mid j \in \mathrm{jobs} \ \rbrace\]

maximum number of simultaneous tasks

\[\sum_m \sum_j \mathrm{step}(\mathrm{start}_j^m) - \mathrm{step}(\mathrm{start}_j^m + \mathrm{Duration}_j^m) \leq \mathrm{Op}\]

Jobshop with arbitrary precedences

Instead of having precedences only within the tasks of a job, there is a more general precedence graph

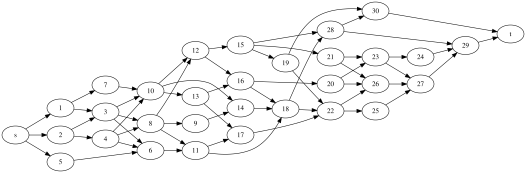
Precedence graph

Jobshop with sequence dependent setup times

There are setup times in the machines to switch from one job to another

Notice that this variant is only interesting if the setup times are sequence-dependent. Otherwise it is equivalent to increase each task by the length of the setup time and to solve an usual jobshop

Flexible jobshop

The tasks of a job can be processed by any machine in a predefined group of similar machines.

Please refer to the flexible-jobshop section of this benchmark for more information

JSPLib solutions - The State-Of-The-Art

In this section are collected the best known solutions (upper bound and lower bound) for each problem in the benchmark.

The solutions may come from

Published papers (with reference eg. NS2002), the section publications gives the complete paper info
An engine run by someone else (eg. CPO2015) which results have been published
An engine run by us (CPO, OptalCP, CPSAT) with approximate resolution time

The type of hardware and time required to find the best known solution are difficult to track and compare, in particular for bounds coming from published papers. Which is why

Every time an engine equals a published result the engine appears in the table instead
An approximative timing for reference engines, in particular when the time to find the solution is unusually long

We do not systematically run the instances for very long times on large machines. Most of the instances that appear as having been solved after a large comptation time (eg. 40h) had peculiarities (e.g. best lb + 1 == best ub) that justified exploring how long it would take to solve them to optimality. We also devote more effort to solve instances which best known solutions are given by papers that are old, difficult to find and difficlt to reproduce. This allows verifying the paper claims and having a more accessible way of generating the result.

Best known solutions - JSPLib

Fisher and Thompson (1963)

FT instances are also known as MT because the 1963 paper of Fisher and Thompson was published in the book “Industrial scheduling” by Muth and Thompson.

Instance	Size	Problem	LB	UB	Type	Solved by
ft06	6 x 6	jobshop	55	55	easy	CPO in < 1 min
ft10	10 x 10	jobshop	930	930	easy	CPO in < 1 min
ft20	20 x 5	jobshop	1165	1165	easy	CPO in < 1 min

Lawrence (1984)

Instance	Size	Problem	LB	UB	Type	Solved by
la01	10 x 5	jobshop	666	666	easy	CPO in < 1 min
la02	10 x 5	jobshop	655	655	easy	CPO in < 1 min
la03	10 x 5	jobshop	597	597	easy	CPO in < 1 min
la04	10 x 5	jobshop	590	590	easy	CPO in < 1 min
la05	10 x 5	jobshop	593	593	easy	CPO in < 1 min
la06	15 x 5	jobshop	926	926	easy	CPO in < 1 min
la07	15 x 5	jobshop	890	890	easy	CPO in < 1 min
la08	15 x 5	jobshop	863	863	easy	CPO in < 1 min
la09	15 x 5	jobshop	951	951	easy	CPO in < 1 min
la10	15 x 5	jobshop	958	958	easy	CPO in < 1 min
la11	20 x 5	jobshop	1222	1222	easy	CPO in < 1 min
la12	20 x 5	jobshop	1039	1039	easy	CPO in < 1 min
la13	20 x 5	jobshop	1150	1150	easy	CPO in < 1 min
la14	20 x 5	jobshop	1292	1292	easy	CPO in < 1 min
la15	20 x 5	jobshop	1207	1207	easy	CPO in < 1 min
la16	10 x 10	jobshop	945	945	easy	CPO in < 1 min
la17	10 x 10	jobshop	784	784	easy	CPO in < 1 min
la18	10 x 10	jobshop	848	848	easy	CPO in < 1 min
la19	10 x 10	jobshop	842	842	easy	CPO in < 1 min
la20	10 x 10	jobshop	902	902	easy	CPO in < 1 min
la21	15 x 10	jobshop	1046	1046	easy	OptalCP in < 1 min
la22	15 x 10	jobshop	927	927	easy	CPO in < 1 min
la23	15 x 10	jobshop	1032	1032	easy	CPO in < 1 min
la24	15 x 10	jobshop	935	935	easy	CPO in < 1 min
la25	15 x 10	jobshop	977	977	easy	CPO in < 1 min
la26	20 x 10	jobshop	1218	1218	easy	CPO in < 1 min
la27	20 x 10	jobshop	1235	1235	easy	OptalCP in < 1 min
la28	20 x 10	jobshop	1216	1216	easy	CPO in < 1 min
la29	20 x 10	jobshop	1152	1152	medium	OptalCP in 5 min
la30	20 x 10	jobshop	1355	1355	easy	CPO in < 1 min
la31	30 x 10	jobshop	1784	1784	easy	CPO in < 1 min
la32	30 x 10	jobshop	1850	1850	easy	CPO in < 1 min
la33	30 x 10	jobshop	1719	1719	easy	CPO in < 1 min
la34	30 x 10	jobshop	1721	1721	easy	CPO in < 1 min
la35	30 x 10	jobshop	1888	1888	easy	CPO in < 1 min
la36	15 x 15	jobshop	1268	1268	easy	CPO in < 1 min
la37	15 x 15	jobshop	1397	1397	easy	CPO in < 1 min
la38	15 x 15	jobshop	1196	1196	easy	OptalCP in < 1 min
la39	15 x 15	jobshop	1233	1233	easy	CPO in < 1 min
la40	15 x 15	jobshop	1222	1222	easy	OptalCP in < 1 min

Adams, Balas and Zawack (1988)

Instance	Size	Problem	LB	UB	Type	Solved by
abz5	10 x 10	jobshop	1234	1234	easy	CPO in < 1 min
abz6	10 x 10	jobshop	943	943	easy	CPO in < 1 min
abz7	20 x 15	jobshop	656	656	medium	OptalCP in < 1h
abz8	20 x 15	jobshop	667	667	hard	OptalCP in 10h
abz9	20 x 15	jobshop	678	678	medium	OptalCP in < 1h

Various places report that “Henning A (2002). Praktische Job-Shop Scheduling-Probleme. Ph.D. thesis, Friedrich-Schiller-Universität Jena, Jena, Germany” as having found a solution of 665 for abz8, but the original document says their solution is 667 and 665 is a “solution from the literature”. We believe it is just a typing mistake in the sources they used. In any case OptalCP proves a lower bound of 667.

Applegate and Cook (1991)

Instance	Size	Problem	LB	UB	Type	Solved by
orb01	10 x 10	jobshop	1059	1059	easy	CPO in < 1 min
orb02	10 x 10	jobshop	888	888	easy	CPO in < 1 min
orb03	10 x 10	jobshop	1005	1005	easy	CPO in < 1 min
orb04	10 x 10	jobshop	1005	1005	easy	CPO in < 1 min
orb05	10 x 10	jobshop	887	887	easy	CPO in < 1 min
orb06	10 x 10	jobshop	1010	1010	easy	CPO in < 1 min
orb07	10 x 10	jobshop	397	397	easy	CPO in < 1 min
orb08	10 x 10	jobshop	899	899	easy	CPO in < 1 min
orb09	10 x 10	jobshop	934	934	easy	CPO in < 1 min
orb10	10 x 10	jobshop	944	944	easy	CPO in < 1 min

Yamada Nakano (1992)

Instance	Size	Problem	LB	UB	Type	Solved by
yn1	20 x 20	jobshop	884	884	hard	OptalCP in 6h
yn2	20 x 20	jobshop	904	904	hard	OptalCP in 40h
yn3	20 x 20	jobshop	892	892	hard	OptalCP in 40h
yn4	20 x 20	jobshop	967	967	hard	OptalCP in 16h

Storer, Wu and Vaccari (1992)

Instance	Size	Problem	LB	UB	Type	Solved by
swv01	20 x 10	jobshop	1407	1407	easy	OptalCP in < 1 min
swv02	20 x 10	jobshop	1475	1475	easy	OptalCP in < 1 min
swv03	20 x 10	jobshop	1398	1398	medium	CPO in < 1h
swv04	20 x 10	jobshop	1464	1464	medium	OptalCP in < 1h
swv05	20 x 10	jobshop	1424	1424	medium	OptalCP in < 1h
swv06	20 x 15	jobshop	1667	1667	hard	OptalCP in 40h
swv07	20 x 15	jobshop	1541	1594	open	lb OptalCP / ub GR2014
swv08	20 x 15	jobshop	1694	1751	open	lb OptalCP / ub Mu2015
swv09	20 x 15	jobshop	1655	1655	hard	OptalCP in 15h
swv10	20 x 15	jobshop	1692	1743	open	lb OptalCP / ub SS2018
swv11	50 x 10	jobshop	2983	2983	medium	OptalCP in < 1h
swv12	50 x 10	jobshop	2972	2972	medium	OptalCP in < 1h
swv13	50 x 10	jobshop	3104	3104	medium	OptalCP in < 1h
swv14	50 x 10	jobshop	2968	2968	medium	CPO in < 1h
swv15	50 x 10	jobshop	2885	2885	hard	OptalCP in 9h
swv16	50 x 10	jobshop	2924	2924	easy	CPO in < 1 min
swv17	50 x 10	jobshop	2794	2794	easy	CPO in < 1 min
swv18	50 x 10	jobshop	2852	2852	easy	CPO in < 1 min
swv19	50 x 10	jobshop	2843	2843	easy	CPO in < 1 min
swv20	50 x 10	jobshop	2823	2823	easy	CPO in < 1 min

Taillard (1993)

Instance	Size	Problem	LB	UB	Type	Solved by
ta01js	15 x 15	jobshop	1231	1231	easy	CPO in < 1 min
ta02js	15 x 15	jobshop	1244	1244	easy	OptalCP in < 1 min
ta03js	15 x 15	jobshop	1218	1218	easy	OptalCP in < 1 min
ta04js	15 x 15	jobshop	1175	1175	easy	OptalCP in < 1 min
ta05js	15 x 15	jobshop	1224	1224	easy	OptalCP in < 1 min
ta06js	15 x 15	jobshop	1238	1238	easy	OptalCP in < 1 min
ta07js	15 x 15	jobshop	1227	1227	easy	OptalCP in < 1 min
ta08js	15 x 15	jobshop	1217	1217	easy	OptalCP in < 1 min
ta09js	15 x 15	jobshop	1274	1274	easy	OptalCP in < 1 min
ta10js	15 x 15	jobshop	1241	1241	easy	OptalCP in < 1 min
ta11js	20 x 15	jobshop	1357	1357	medium	OptalCP in < 1h
ta12js	20 x 15	jobshop	1367	1367	medium	OptalCP in < 1h
ta13js	20 x 15	jobshop	1342	1342	medium	OptalCP in < 1h
ta14js	20 x 15	jobshop	1345	1345	easy	CPO in < 1 min
ta15js	20 x 15	jobshop	1339	1339	medium	OptalCP in < 1h
ta16js	20 x 15	jobshop	1360	1360	medium	OptalCP in < 1h
ta17js	20 x 15	jobshop	1462	1462	easy	OptalCP in < 1 min
ta18js	20 x 15	jobshop	1396	1396	medium	OptalCP in < 1h
ta19js	20 x 15	jobshop	1332	1332	medium	OptalCP in < 1h
ta20js	20 x 15	jobshop	1348	1348	medium	OptalCP in < 1h
ta21js	20 x 20	jobshop	1642	1642	medium	OptalCP < 1h
ta22js	20 x 20	jobshop	1600	1600	hard	OptalCP in 2h
ta23js	20 x 20	jobshop	1557	1557	hard	OptalCP in 2h
ta24js	20 x 20	jobshop	1644	1644	medium	OptalCP in < 1h
ta25js	20 x 20	jobshop	1595	1595	medium	OptalCP in < 1h
ta26js	20 x 20	jobshop	1643	1643	medium	OptalCP in 7h
ta27js	20 x 20	jobshop	1680	1680	medium	OptalCP in < 1h
ta28js	20 x 20	jobshop	1603	1603	medium	OptalCP in < 1h
ta29js	20 x 20	jobshop	1625	1625	hard	OptalCP in 2h
ta30js	20 x 20	jobshop	1562	1584	open	lb OptalCP / ub NS2002
ta31js	30 x 15	jobshop	1764	1764	medium	CPO in < 1h
ta32js	30 x 15	jobshop	1774	1784	open	lb CPO2015 / ub PSV2010
ta33js	30 x 15	jobshop	1791	1791	hard	OptalCP in 10h
ta34js	30 x 15	jobshop	1828	1828	medium	OptalCP in < 1h
ta35js	30 x 15	jobshop	2007	2007	easy	OptalCP in < 1 min
ta36js	30 x 15	jobshop	1819	1819	medium	OptalCP in < 1h
ta37js	30 x 15	jobshop	1771	1771	hard	OptalCP in 2h
ta38js	30 x 15	jobshop	1673	1673	hard	OptalCP in 7h
ta39js	30 x 15	jobshop	1795	1795	easy	OptalCP in < 1 min
ta40js	30 x 15	jobshop	1658	1669	open	lb OptalCP / ub GR2014
ta41js	30 x 20	jobshop	1926	2005	open	lb OptalCP / ub CPO2015
ta42js	30 x 20	jobshop	1900	1937	open	lb OptalCP / ub GR2014
ta43js	30 x 20	jobshop	1809	1846	open	lb CPO2015 / ub PLC2015
ta44js	30 x 20	jobshop	1961	1979	open	lb OptalCP / ub CS2022
ta45js	30 x 20	jobshop	1997	1997	medium	OptalCP in < 1h
ta46js	30 x 20	jobshop	1976	2004	open	lb OptalCP / ub GR2014
ta47js	30 x 20	jobshop	1827	1889	open	lb OptalCP / ub PLC2015
ta48js	30 x 20	jobshop	1921	1937	open	lb OptalCP / ub SS2018
ta49js	30 x 20	jobshop	1938	1960	open	lb OptalCP / ub LHW2024
ta50js	30 x 20	jobshop	1848	1923	open	lb OptalCP / ub PLC2015
ta51js	50 x 15	jobshop	2760	2760	easy	CPO in < 1 min
ta52js	50 x 15	jobshop	2756	2756	easy	OptalCP in < 1 min
ta53js	50 x 15	jobshop	2717	2717	easy	OptalCP in < 1 min
ta54js	50 x 15	jobshop	2839	2839	easy	CPO in < 1 min
ta55js	50 x 15	jobshop	2679	2679	easy	OptalCP in < 1 min
ta56js	50 x 15	jobshop	2781	2781	easy	OptalCP in < 1 min
ta57js	50 x 15	jobshop	2943	2943	easy	CPO in < 1 min
ta58js	50 x 15	jobshop	2885	2885	easy	CPO in < 1 min
ta59js	50 x 15	jobshop	2655	2655	easy	OptalCP in < 1 min
ta60js	50 x 15	jobshop	2723	2723	easy	OptalCP in < 1 min
ta61js	50 x 20	jobshop	2868	2868	easy	OptalCP in < 1 min
ta62js	50 x 20	jobshop	2869	2869	medium	OptalCP in < 1h
ta63js	50 x 20	jobshop	2755	2755	easy	OptalCP in < 1 min
ta64js	50 x 20	jobshop	2702	2702	easy	OptalCP in < 1 min
ta65js	50 x 20	jobshop	2725	2725	easy	OptalCP in < 1 min
ta66js	50 x 20	jobshop	2845	2845	easy	OptalCP in < 1 min
ta67js	50 x 20	jobshop	2825	2825	hard	OptalCP in 4h
ta68js	50 x 20	jobshop	2784	2784	easy	OptalCP in < 1 min
ta69js	50 x 20	jobshop	3071	3071	easy	OptalCP in < 1 min
ta70js	50 x 20	jobshop	2995	2995	medium	CPO in < 1h
ta71js	100 x 20	jobshop	5464	5464	easy	OptalCP in < 1 min
ta72js	100 x 20	jobshop	5181	5181	easy	OptalCP in < 1 min
ta73js	100 x 20	jobshop	5568	5568	easy	OptalCP in < 1 min
ta74js	100 x 20	jobshop	5339	5339	easy	OptalCP in < 1 min
ta75js	100 x 20	jobshop	5392	5392	medium	CPO in < 1h
ta76js	100 x 20	jobshop	5342	5342	easy	OptalCP in < 1 min
ta77js	100 x 20	jobshop	5436	5436	easy	OptalCP in < 1 min
ta78js	100 x 20	jobshop	5394	5394	easy	OptalCP in < 1 min
ta79js	100 x 20	jobshop	5358	5358	easy	OptalCP in < 1 min
ta80js	100 x 20	jobshop	5183	5183	easy	OptalCP in < 1 min

Demikol, Mehta and Uzsoy (1998)

Instance	Size	Problem	LB	UB	Type	Solved by
dmu01	20 x 15	jobshop	2563	2563	medium	OptalCP in < 1h
dmu02	20 x 15	jobshop	2706	2706	medium	OptalCP in < 1h
dmu03	20 x 15	jobshop	2731	2731	medium	CPO in < 1h
dmu04	20 x 15	jobshop	2669	2669	medium	OptalCP in < 1h
dmu05	20 x 15	jobshop	2749	2749	medium	OptalCP in < 1h
dmu06	20 x 20	jobshop	3244	3244	hard	OptalCP in 2h
dmu07	20 x 20	jobshop	3046	3046	hard	OptalCP in 3h
dmu08	20 x 20	jobshop	3188	3188	medium	OptalCP in < 1h
dmu09	20 x 20	jobshop	3092	3092	medium	OptalCP in < 1h
dmu10	20 x 20	jobshop	2984	2984	medium	OptalCP in < 1h
dmu11	30 x 15	jobshop	3402	3430	open	lb OptalCP / ub PLC2015
dmu12	30 x 15	jobshop	3481	3492	open	lb OptalCP / ub SS2018
dmu13	30 x 15	jobshop	3681	3681	hard	OptalCP in 3h
dmu14	30 x 15	jobshop	3394	3394	easy	OptalCP in < 1 min
dmu15	30 x 15	jobshop	3343	3343	easy	OptalCP in < 1 min
dmu16	30 x 20	jobshop	3734	3750	open	lb CPO2015 / ub LHW2024
dmu17	30 x 20	jobshop	3733	3812	open	lb OptalCP / ub LHW2024
dmu18	30 x 20	jobshop	3844	3844	hard	OptalCP in 10h
dmu19	30 x 20	jobshop	3707	3764	open	lb OptalCP / ub CS2022
dmu20	30 x 20	jobshop	3632	3699	open	lb OptalCP / ub LHW2024
dmu21	40 x 15	jobshop	4380	4380	easy	OptalCP in < 1 min
dmu22	40 x 15	jobshop	4725	4725	easy	CPO in < 1 min
dmu23	40 x 15	jobshop	4668	4668	easy	CPO in < 1 min
dmu24	40 x 15	jobshop	4648	4648	easy	CPO in < 1 min
dmu25	40 x 15	jobshop	4164	4164	easy	CPO in < 1 min
dmu26	40 x 20	jobshop	4647	4647	medium	OptalCP < 1h
dmu27	40 x 20	jobshop	4848	4848	medium	OptalCP in < 1h
dmu28	40 x 20	jobshop	4692	4692	easy	OptalCP in < 1 min
dmu29	40 x 20	jobshop	4691	4691	easy	OptalCP in < 1 min
dmu30	40 x 20	jobshop	4732	4732	medium	OptalCP < 1h
dmu31	50 x 15	jobshop	5640	5640	easy	CPO in < 1 min
dmu32	50 x 15	jobshop	5927	5927	easy	CPO in < 1 min
dmu33	50 x 15	jobshop	5728	5728	easy	CPO in < 1 min
dmu34	50 x 15	jobshop	5385	5385	easy	CPO in < 1 min
dmu35	50 x 15	jobshop	5635	5635	easy	CPO in < 1 min
dmu36	50 x 20	jobshop	5621	5621	easy	OptalCP in < 1 min
dmu37	50 x 20	jobshop	5851	5851	medium	CPO in < 1h
dmu38	50 x 20	jobshop	5713	5713	medium	OptalCP in < 1h
dmu39	50 x 20	jobshop	5747	5747	easy	OptalCP in < 1 min
dmu40	50 x 20	jobshop	5577	5577	easy	OptalCP in < 1 min
dmu41	20 x 15	jobshop	3176	3248	open	lb OptalCP / ub PLC2015
dmu42	20 x 15	jobshop	3339	3390	open	lb OptalCP / ub SS2018
dmu43	20 x 15	jobshop	3441	3441	hard	OptalCP in 8h
dmu44	20 x 15	jobshop	3414	3475	open	lb OptalCP / ub SS2018
dmu45	20 x 15	jobshop	3217	3266	open	lb OptalCP / ub CS2022
dmu46	20 x 20	jobshop	3780	4035	open	lb OptalCP / ub GR2014
dmu47	20 x 20	jobshop	3714	3939	open	lb OptalCP / ub GR2014
dmu48	20 x 20	jobshop	3628	3763	open	lb OptalCP / ub SS2018
dmu49	20 x 20	jobshop	3543	3706	open	lb OptalCP / ub LHW2024
dmu50	20 x 20	jobshop	3618	3729	open	lb OptalCP / ub PLC2015
dmu51	30 x 15	jobshop	4070	4156	open	lb OptalCP / ub SS2018
dmu52	30 x 15	jobshop	4203	4297	open	lb OptalCP / ub LHW2024
dmu53	30 x 15	jobshop	4248	4378	open	lb OptalCP / ub CS2022
dmu54	30 x 15	jobshop	4277	4361	open	lb OptalCP / ub CS2022
dmu55	30 x 15	jobshop	4191	4258	open	lb OptalCP / ub LHW2024
dmu56	30 x 20	jobshop	4755	4939	open	lb OptalCP / ub XLGG2022
dmu57	30 x 20	jobshop	4462	4647	open	lb OptalCP / ub XLGG2022
dmu58	30 x 20	jobshop	4484	4701	open	lb OptalCP / ub CS2022
dmu59	30 x 20	jobshop	4366	4607	open	lb OptalCP / ub LHW2024
dmu60	30 x 20	jobshop	4468	4721	open	lb OptalCP / ub CS2022
dmu61	40 x 15	jobshop	5038	5169	open	lb OptalCP / ub LHW2024
dmu62	40 x 15	jobshop	5176	5247	open	lb OptalCP / ub LHW2024
dmu63	40 x 15	jobshop	5245	5312	open	lb OptalCP / ub LHW2024
dmu64	40 x 15	jobshop	5155	5226	open	lb OptalCP / ub CS2022
dmu65	40 x 15	jobshop	5122	5173	open	lb OptalCP / ub LHW2024
dmu66	40 x 20	jobshop	5526	5701	open	lb OptalCP / ub CS2022
dmu67	40 x 20	jobshop	5661	5779	open	lb OptalCP / ub SS2018
dmu68	40 x 20	jobshop	5513	5763	open	lb OptalCP / ub CS2022
dmu69	40 x 20	jobshop	5511	5688	open	lb OptalCP / ub CS2022
dmu70	40 x 20	jobshop	5633	5868	open	lb OptalCP / ub CS2022
dmu71	50 x 15	jobshop	6129	6207	open	lb OptalCP / ub CS2022
dmu72	50 x 15	jobshop	6434	6463	open	lb CdGKGC2025 / ub SS2018
dmu73	50 x 15	jobshop	6107	6136	open	lb OptalCP / ub CS2022
dmu74	50 x 15	jobshop	6168	6196	open	lb OptalCP / ub SS2018
dmu75	50 x 15	jobshop	6123	6189	open	lb OptalCP / ub SS2018
dmu76	50 x 20	jobshop	6479	6718	open	lb OptalCP / ub CS2022
dmu77	50 x 20	jobshop	6520	6747	open	lb OptalCP / ub CS2022
dmu78	50 x 20	jobshop	6643	6755	open	lb OptalCP / ub CS2022
dmu79	50 x 20	jobshop	6720	6910	open	lb OptalCP / ub CS2022
dmu80	50 x 20	jobshop	6460	6634	open	lb OptalCP / ub CS2022

Da Col and Teppan (2022)

Instance	Size	Problem	LB	UB	Type	Solved by
tai_j10_m10_1	10 x 10	jobshop	8219	8219	easy	OptalCP in < 1 min
tai_j10_m10_2	10 x 10	jobshop	7416	7416	easy	OptalCP in < 1 min
tai_j10_m10_3	10 x 10	jobshop	8094	8094	easy	OptalCP in < 1 min
tai_j10_m10_4	10 x 10	jobshop	8657	8657	easy	OptalCP in < 1 min
tai_j10_m10_5	10 x 10	jobshop	7936	7936	easy	OptalCP in < 1 min
tai_j10_m10_6	10 x 10	jobshop	8509	8509	easy	OptalCP in < 1 min
tai_j10_m10_7	10 x 10	jobshop	8299	8299	easy	OptalCP in < 1 min
tai_j10_m10_8	10 x 10	jobshop	7788	7788	easy	OptalCP in < 1 min
tai_j10_m10_9	10 x 10	jobshop	8300	8300	easy	OptalCP in < 1 min
tai_j10_m10_10	10 x 10	jobshop	8481	8481	easy	OptalCP in < 1 min
tai_j10_m100_1	10 x 100	jobshop	56609	56609	easy	OptalCP in < 1 min
tai_j10_m100_2	10 x 100	jobshop	52330	52330	easy	OptalCP in < 1 min
tai_j10_m100_3	10 x 100	jobshop	56412	56412	easy	OptalCP in < 1 min
tai_j10_m100_4	10 x 100	jobshop	54889	54889	easy	OptalCP in < 1 min
tai_j10_m100_5	10 x 100	jobshop	54603	54603	easy	OptalCP in < 1 min
tai_j10_m100_6	10 x 100	jobshop	53723	53723	easy	OptalCP in < 1 min
tai_j10_m100_7	10 x 100	jobshop	55456	55456	easy	OptalCP in < 1 min
tai_j10_m100_8	10 x 100	jobshop	56466	56466	easy	OptalCP in < 1 min
tai_j10_m100_9	10 x 100	jobshop	55096	55096	easy	OptalCP in < 1 min
tai_j10_m100_10	10 x 100	jobshop	56661	56661	easy	OptalCP in < 1 min
tai_j10_m1000_1	10 x 1000	jobshop	515370	515370	easy	OptalCP in < 1 min
tai_j10_m1000_2	10 x 1000	jobshop	513525	513525	easy	OptalCP in < 1 min
tai_j10_m1000_3	10 x 1000	jobshop	508161	508161	easy	OptalCP in < 1 min
tai_j10_m1000_4	10 x 1000	jobshop	513814	513814	easy	OptalCP in < 1 min
tai_j10_m1000_5	10 x 1000	jobshop	517020	517020	easy	OptalCP in < 1 min
tai_j10_m1000_6	10 x 1000	jobshop	517777	517777	easy	OptalCP in < 1 min
tai_j10_m1000_7	10 x 1000	jobshop	514921	514921	easy	OptalCP in < 1 min
tai_j10_m1000_8	10 x 1000	jobshop	522277	522277	easy	OptalCP in < 1 min
tai_j10_m1000_9	10 x 1000	jobshop	511213	511213	easy	OptalCP in < 1 min
tai_j10_m1000_10	10 x 1000	jobshop	509855	509855	easy	OptalCP in < 1 min
tai_j100_m10_1	100 x 10	jobshop	54951	54951	easy	OptalCP in < 1 min
tai_j100_m10_2	100 x 10	jobshop	57160	57160	easy	OptalCP in < 1 min
tai_j100_m10_3	100 x 10	jobshop	54166	54166	easy	OptalCP in < 1 min
tai_j100_m10_4	100 x 10	jobshop	54371	54371	easy	OptalCP in < 1 min
tai_j100_m10_5	100 x 10	jobshop	56142	56142	easy	OptalCP in < 1 min
tai_j100_m10_6	100 x 10	jobshop	52447	52447	easy	OptalCP in < 1 min
tai_j100_m10_7	100 x 10	jobshop	54051	54051	easy	OptalCP in < 1 min
tai_j100_m10_8	100 x 10	jobshop	55624	55624	easy	OptalCP in < 1 min
tai_j100_m10_9	100 x 10	jobshop	54210	54210	easy	OptalCP in < 1 min
tai_j100_m10_10	100 x 10	jobshop	55464	55464	easy	OptalCP in < 1 min
tai_j100_m100_1	100 x 100	jobshop	62843	77127	open	OptalCP
tai_j100_m100_2	100 x 100	jobshop	62814	77322	open	OptalCP
tai_j100_m100_3	100 x 100	jobshop	61533	76910	open	OptalCP
tai_j100_m100_4	100 x 100	jobshop	64742	78604	open	OptalCP
tai_j100_m100_5	100 x 100	jobshop	61766	78023	open	OptalCP
tai_j100_m100_6	100 x 100	jobshop	61360	77895	open	OptalCP
tai_j100_m100_7	100 x 100	jobshop	64040	77670	open	OptalCP
tai_j100_m100_8	100 x 100	jobshop	63224	78031	open	OptalCP
tai_j100_m100_9	100 x 100	jobshop	62631	79419	open	OptalCP
tai_j100_m100_10	100 x 100	jobshop	64866	77837	open	OptalCP
tai_j100_m1000_1	100 x 1000	jobshop	522298	544732	open	OptalCP
tai_j100_m1000_2	100 x 1000	jobshop	530375	546598	open	OptalCP
tai_j100_m1000_3	100 x 1000	jobshop	530560	549372	open	OptalCP
tai_j100_m1000_4	100 x 1000	jobshop	527101	545138	open	OptalCP
tai_j100_m1000_5	100 x 1000	jobshop	517728	545535	open	OptalCP
tai_j100_m1000_6	100 x 1000	jobshop	522907	545730	open	OptalCP
tai_j100_m1000_7	100 x 1000	jobshop	522537	546899	open	OptalCP
tai_j100_m1000_8	100 x 1000	jobshop	526428	549337	open	OptalCP
tai_j100_m1000_9	100 x 1000	jobshop	528097	550693	open	OptalCP
tai_j100_m1000_10	100 x 1000	jobshop	521766	543797	open	OptalCP
tai_j1000_m10_1	1000 x 10	jobshop	515334	515334	easy	OptalCP in < 1 min
tai_j1000_m10_2	1000 x 10	jobshop	509226	509226	easy	OptalCP in < 1 min
tai_j1000_m10_3	1000 x 10	jobshop	517493	517493	easy	OptalCP in < 1 min
tai_j1000_m10_4	1000 x 10	jobshop	519369	519369	easy	OptalCP in < 1 min
tai_j1000_m10_5	1000 x 10	jobshop	513881	513881	easy	OptalCP in < 1 min
tai_j1000_m10_6	1000 x 10	jobshop	511932	511932	easy	OptalCP in < 1 min
tai_j1000_m10_7	1000 x 10	jobshop	523900	523900	easy	OptalCP in < 1 min
tai_j1000_m10_8	1000 x 10	jobshop	513101	513101	easy	OptalCP in < 1 min
tai_j1000_m10_9	1000 x 10	jobshop	508701	508701	easy	OptalCP in < 1 min
tai_j1000_m10_10	1000 x 10	jobshop	521360	521360	easy	OptalCP in < 1 min
tai_j1000_m100_1	1000 x 100	jobshop	525343	539120	open	OptalCP
tai_j1000_m100_2	1000 x 100	jobshop	528088	540895	open	OptalCP
tai_j1000_m100_3	1000 x 100	jobshop	522793	534794	open	OptalCP
tai_j1000_m100_4	1000 x 100	jobshop	524271	536317	open	OptalCP
tai_j1000_m100_5	1000 x 100	jobshop	531216	532016	open	OptalCP
tai_j1000_m100_6	1000 x 100	jobshop	518763	535189	open	OptalCP
tai_j1000_m100_7	1000 x 100	jobshop	527093	535894	open	OptalCP
tai_j1000_m100_8	1000 x 100	jobshop	519524	533985	open	OptalCP
tai_j1000_m100_9	1000 x 100	jobshop	520889	539511	open	OptalCP
tai_j1000_m100_10	1000 x 100	jobshop	529112	540884	open	OptalCP
tai_j1000_m1000_1	1000 x 1000	jobshop	549392	877062	open	lb OptalCP / ub Hexaly2024
tai_j1000_m1000_2	1000 x 1000	jobshop	549043	877115	open	lb OptalCP / ub Hexaly2024
tai_j1000_m1000_3	1000 x 1000	jobshop	552580	878805	open	lb OptalCP / ub Hexaly2024
tai_j1000_m1000_4	1000 x 1000	jobshop	547670	876363	open	lb OptalCP / ub Hexaly2024
tai_j1000_m1000_5	1000 x 1000	jobshop	545193	877562	open	lb OptalCP / ub Hexaly2024
tai_j1000_m1000_6	1000 x 1000	jobshop	547286	876067	open	lb OptalCP / ub Hexaly2024
tai_j1000_m1000_7	1000 x 1000	jobshop	545877	875891	open	lb OptalCP / ub Hexaly2024
tai_j1000_m1000_8	1000 x 1000	jobshop	549220	876456	open	lb OptalCP / ub Hexaly2024
tai_j1000_m1000_9	1000 x 1000	jobshop	543559	875914	open	lb OptalCP / ub Hexaly2024
tai_j1000_m1000_10	1000 x 1000	jobshop	541530	874820	open	lb OptalCP / ub Hexaly2024

DaCol and Teppan - reentrant jobshop (2022)

Instance	Size	Problem	LB	UB	Type	Solved by
long-100-10000-1	103 x 100	reentrant jobshop	600000	600000	easy	OptalCP in < 1 min
long-100-10000-2	103 x 100	reentrant jobshop	600000	600000	easy	OptalCP in < 1 min
long-100-10000-3	103 x 100	reentrant jobshop	600000	600000	easy	OptalCP in < 1 min
long-100-100000-1	109 x 100	reentrant jobshop	600000	600000	easy	OptalCP in < 1 min
long-100-100000-2	114 x 100	reentrant jobshop	600000	600000	medium	OptalCP in < 1h
long-100-100000-3	109 x 100	reentrant jobshop	600000	600000	easy	OptalCP in < 1 min
long-1000-10000-1	1002 x 1000	reentrant jobshop	600000	600000	easy	OptalCP in < 1 min
long-1000-10000-2	1002 x 1000	reentrant jobshop	600000	600000	easy	OptalCP in < 1 min
long-1000-10000-3	1002 x 1000	reentrant jobshop	600000	600000	easy	OptalCP in < 1 min
long-1000-100000-1	1002 x 1000	reentrant jobshop	600000	600000	easy	OptalCP in < 1 min
long-1000-100000-2	1002 x 1000	reentrant jobshop	600000	600000	easy	OptalCP in < 1 min
long-1000-100000-3	1003 x 1000	reentrant jobshop	600000	600000	easy	OptalCP in < 1 min

Instance	Size	Problem	LB	UB	Type	Solved by
short-100-10000-1	2162 x 100	reentrant jobshop	600000	600000	easy	OptalCP in < 1 min
short-100-10000-2	2192 x 100	reentrant jobshop	600000	600000	easy	OptalCP in < 1 min
short-100-10000-3	2169 x 100	reentrant jobshop	600000	600000	easy	OptalCP in < 1 min
short-100-100000-1	20685 x 100	reentrant jobshop	600000	600000	medium	OptalCP in < 1h
short-100-100000-2	20870 x 100	reentrant jobshop	600000	600000	medium	OptalCP in < 1h
short-100-100000-3	20767 x 100	reentrant jobshop	600000	600000	medium	OptalCP in < 1h
short-1000-10000-1	2882 x 1000	reentrant jobshop	600000	600000	easy	OptalCP in < 1 min
short-1000-10000-2	2863 x 1000	reentrant jobshop	600000	600000	easy	OptalCP in < 1 min
short-1000-10000-3	2897 x 1000	reentrant jobshop	600000	600000	medium	OptalCP in < 1h
short-1000-100000-1	21280 x 1000	reentrant jobshop	600000	600038	open	OptalCP
short-1000-100000-2	21349 x 1000	reentrant jobshop	600000	600000	medium	OptalCP in < 1h
short-1000-100000-3	21338 x 1000	reentrant jobshop	600000	600000	medium	OptalCP in < 1h

DaCol and Tepan report instance short-1000-100000-1 was solved to optimality by CP Optimizer in 6h which we haven’t been able to reproduce (with CPO any other solver). We are still investigating

Publications (best known solutions)

The upper and lower bounds come from

NS2002 (1 bound - ta30js) : Nowicki, E., & Smutnicki, C. (2002). Some new tools to solve the job shop problem. Raport serii: Preprinty, 60.
PSV2010 (1 bound - ta32js) : Pardalos, P. M., Shylo, O. V., & Vazacopoulos, A. (2010). Solving job shop scheduling problems utilizing the properties of backbone and “big valley”. Computational Optimization and Applications, 47, 61-76.
GR2014 (6 bounds in dmu, swv and ta) : Gonçalves, J. F., & Resende, M. G. (2014). An extended Akers graphical method with a biased random‐key genetic algorithm for job‐shop scheduling. International Transactions in Operational Research, 21(2), 215-246.
CPO2015 (4 bounds in dmu and ta) :
- Vilím, P., Laborie, P., & Shaw, P. (2015). Failure-directed search for constraint-based scheduling. In CPAIOR 2015 proceedings.
- Vilím, P., Laborie, P., & Shaw, P.. Detailed experimental results.
Mu2015 (1 bound - swv08) : Personal communication to optimizizer, probably based on Murovec, B. (2015). Job-shop local-search move evaluation without direct consideration of the criterion’s value. European Journal of Operational Research, 241(2), 320-329.
PLC2015 (6 bounds in dmu and ta) : Peng, B., Lü, Z., & Cheng, T. C. E. (2015). A tabu search/path relinking algorithm to solve the job shop scheduling problem. Computers & Operations Research, 53, 154-164.
SS2018 (11 bounds in dmu, swv and ta) : Shylo, O. V., & Shams, H. (2018). Boosting binary optimization via binary classification: A case study of job shop scheduling.
CS2022 (19 bounds in dmu and ta) : Constantino, O. H., & Segura, C. (2022). A parallel memetic algorithm with explicit management of diversity for the job shop scheduling problem. Applied Intelligence, 52(1), 141-153.
XLGG2022 (2 bounds in dmu) : Xie, J., Li, X., Gao, L., & Gui, L. (2022). A hybrid algorithm with a new neighborhood structure for job shop scheduling problems. Computers & Industrial Engineering, 169, 108205.
Hexaly2024 (10 bounds in tai) : Lea Blaise (2014). Hexaly benchmarks and comparisons.
LHW2024 (12 bounds in dmu and ta) : Mingjie Li, Jin-Kao Hao & Qinghua Wu (2025). Combining Hash-based Tabu Search and Frequent Pattern Mining for Job-Shop Scheduling. IISE Transactions.
CdGKGC2025 (1 bound - dmu72) : Marc-Emmanuel Coupvent des Graviers, Lotfi Kobrosly, Christophe Guettier, and Tristan Cazenave (2025). Updating Lower and Upper Bounds for the Job-Shop Scheduling Problem Test Instances.

All other bounds were found by OptalCP

Comparison of reference engines

We provide these tests as a reference, you should get something similar on your hardware (multi-core engines are inherently non-deterministic hence each run returns slightly different results) or find an explanation of why the engines don’t behave as expected. We strongly encourage you to run all engines you want to compare against on your own hardware.

The instances used for the comparison may change on a regular basis

ABZ instances

On an Windows PC with an i7 4-core 3.3GHz 32GB ram in 600 seconds

OptalCP Academic Version 2026.2.0 default search
CP-SAT V9.15.6755 with default configuration
CPO 22.1.1.0

Instance	OptalCP	CP-SAT
abz5	1234 in 0s	1234 in 1s
abz6	943 in 0s	943 in 1s
abz7	656 in 224s	656..657 in 600s
abz8	642..674 in 600s	630..683 in 600s
abz9	670..678 in 600s	655..689 in 600s

SWV instances

On an Windows PC with an i7 4-core 3.3GHz 32GB ram in 600 seconds

OptalCP Academic Version 2026.2.0 default search
CP-SAT V9.15.6755 with default configuration
CPO 22.1.1.0

Instance	OptalCP	CP-SAT
swv01	1407 in 70s	1402..1418 in 600s
swv02	1475 in 12s	1475 in 89s
swv03	1398 in 213s	1387..1413 in 600s
swv04	1453..1478 in 600s	1440..1510 in 600s
swv05	1424 in 148s	1414..1429 in 600s
swv06	1619..1700 in 600s	1601..1696 in 600s
swv07	1479..1628 in 600s	1470..1669 in 600s
swv08	1640..1786 in 600s	1640..1830 in 600s
swv09	1622..1684 in 600s	1611..1696 in 600s
swv10	1649..1783 in 600s	1631..1785 in 600s
swv11	2983..2993 in 600s	2983..3155 in 600s
swv12	2972..3000 in 600s	2972..3094 in 600s
swv13	3104 in 37s	3104..3142 in 600s
swv14	2968 in 9s	2968..3110 in 600s
swv15	2885..2887 in 600s	2885..3066 in 600s
swv16	2924 in 0s	2924 in 0s
swv17	2794 in 0s	2794 in 0s
swv18	2852 in 0s	2852 in 0s
swv19	2843 in 0s	2843 in 3s
swv20	2823 in 0s	2823 in 0s

DMU instances 1-40

On an Windows PC with an i7 4-core 3.3GHz 32GB ram in 600 seconds

OptalCP Academic Version 2026.2.0 default search
CP-SAT V9.15.6755 with default configuration
CPO 22.1.1.0

Instance	OptalCP	CP-SAT
dmu01	2515..2563 in 600s	2467..2634 in 600s
dmu02	2706 in 416s	2607..2706 in 600s
dmu03	2731 in 162s	2684..2753 in 600s
dmu04	2603..2675 in 600s	2563..2694 in 600s
dmu05	2733..2749 in 600s	2713..2779 in 600s
dmu06	3121..3248 in 600s	3087..3314 in 600s
dmu07	2942..3098 in 600s	2921..3094 in 600s
dmu08	3188 in 595s	3076..3197 in 600s
dmu09	3092 in 346s	3000..3092 in 600s
dmu10	2972..2984 in 600s	2914..2985 in 600s
dmu11	3395..3466 in 600s	3395..3491 in 600s
dmu12	3481..3519 in 600s	3481..3604 in 600s
dmu13	3681..3718 in 600s	3681..3758 in 600s
dmu14	3394 in 131s	3394 in 14s
dmu15	3343 in 129s	3343..3404 in 600s
dmu16	3734..3784 in 600s	3734..3836 in 600s
dmu17	3709..3874 in 600s	3709..3942 in 600s
dmu18	3844..3882 in 600s	3844..3927 in 600s
dmu19	3683..3834 in 600s	3678..3893 in 600s
dmu20	3604..3749 in 600s	3604..3893 in 600s
dmu21	4380 in 1s	4380..4387 in 600s
dmu22	4725 in 2s	4725 in 91s
dmu23	4668 in 1s	4668 in 24s
dmu24	4648 in 1s	4648 in 68s
dmu25	4164 in 1s	4164 in 32s
dmu26	4647..4673 in 600s	4647..4851 in 600s
dmu27	4848 in 17s	4848..4970 in 600s
dmu28	4692 in 8s	4692..4786 in 600s
dmu29	4691 in 5s	4691..4825 in 600s
dmu30	4732..4741 in 600s	4732..4842 in 600s
dmu31	5640 in 2s	5640 in 174s
dmu32	5927 in 0s	5927 in 1s
dmu33	5728 in 1s	5728 in 26s
dmu34	5385 in 1s	5385 in 102s
dmu35	5635 in 1s	5635 in 68s
dmu36	5621 in 11s	5621..5784 in 600s
dmu37	5851 in 11s	5851 in 493s
dmu38	5713 in 20s	5713..5871 in 600s
dmu39	5747 in 10s	5747 in 563s
dmu40	5577 in 6s	5577..5685 in 600s

TA instances 1-80

On an Windows PC with an i7 4-core 3.3GHz 32GB ram in 600 seconds

OptalCP Academic Version 2026.2.0 default search
CP-SAT V9.15.6755 with default configuration
CPO 22.1.1.0

Instance	OptalCP	CP-SAT
ta01js	1231 in 0s	1231 in 11s
ta02js	1244 in 3s	1244 in 80s
ta03js	1218 in 2s	1218 in 20s
ta04js	1175 in 3s	1175 in 19s
ta05js	1224 in 14s	1224 in 120s
ta06js	1238 in 185s	1201..1239 in 600s
ta07js	1227 in 18s	1227 in 476s
ta08js	1217 in 12s	1217 in 77s
ta09js	1274 in 8s	1274 in 284s
ta10js	1241 in 4s	1241 in 32s
ta11js	1337..1358 in 600s	1307..1378 in 600s
ta12js	1367 in 333s	1350..1367 in 600s
ta13js	1317..1344 in 600s	1279..1359 in 600s
ta14js	1345 in 3s	1345 in 13s
ta15js	1323..1349 in 600s	1299..1358 in 600s
ta16js	1339..1360 in 600s	1296..1364 in 600s
ta17js	1462 in 4s	1462 in 62s
ta18js	1366..1402 in 600s	1359..1414 in 600s
ta19js	1318..1334 in 600s	1292..1364 in 600s
ta20js	1329..1350 in 600s	1315..1357 in 600s
ta21js	1619..1651 in 600s	1581..1656 in 600s
ta22js	1555..1615 in 600s	1529..1638 in 600s
ta23js	1512..1565 in 600s	1496..1569 in 600s
ta24js	1644 in 323s	1610..1665 in 600s
ta25js	1561..1610 in 600s	1528..1617 in 600s
ta26js	1571..1670 in 600s	1559..1672 in 600s
ta27js	1629..1699 in 600s	1623..1685 in 600s
ta28js	1603 in 203s	1588..1609 in 600s
ta29js	1577..1625 in 600s	1535..1656 in 600s
ta30js	1484..1607 in 600s	1487..1608 in 600s
ta31js	1764 in 98s	1764..1778 in 600s
ta32js	1774..1824 in 600s	1774..1850 in 600s
ta33js	1786..1801 in 600s	1783..1859 in 600s
ta34js	1828..1846 in 600s	1828..1869 in 600s
ta35js	2007 in 1s	2007 in 7s
ta36js	1819 in 7s	1819..1832 in 600s
ta37js	1771..1779 in 600s	1771..1813 in 600s
ta38js	1673..1682 in 600s	1673..1710 in 600s
ta39js	1795 in 23s	1795 in 75s
ta40js	1645..1695 in 600s	1642..1732 in 600s
ta41js	1882..2038 in 600s	1889..2094 in 600s
ta42js	1878..1968 in 600s	1873..2006 in 600s
ta43js	1809..1894 in 600s	1809..1969 in 600s
ta44js	1944..1993 in 600s	1937..2061 in 600s
ta45js	1997..2005 in 600s	1997 in 424s
ta46js	1958..2047 in 600s	1943..2074 in 600s
ta47js	1801..1937 in 600s	1797..1981 in 600s
ta48js	1912..1975 in 600s	1912..2007 in 600s
ta49js	1925..2012 in 600s	1926..2017 in 600s
ta50js	1822..1970 in 600s	1819..2001 in 600s
ta51js	2760 in 3s	2760 in 196s
ta52js	2756 in 3s	2756 in 141s
ta53js	2717 in 2s	2717 in 53s
ta54js	2839 in 1s	2839 in 26s
ta55js	2679 in 3s	2679 in 216s
ta56js	2781 in 2s	2781 in 69s
ta57js	2943 in 2s	2943 in 43s
ta58js	2885 in 2s	2885 in 114s
ta59js	2655 in 2s	2655 in 131s
ta60js	2723 in 3s	2723 in 184s
ta61js	2868 in 6s	2868..2873 in 600s
ta62js	2869..2872 in 600s	2869..2984 in 600s
ta63js	2755 in 8s	2755..2777 in 600s
ta64js	2702 in 6s	2702..2745 in 600s
ta65js	2725 in 7s	2725..2789 in 600s
ta66js	2845 in 5s	2845..2919 in 600s
ta67js	2825..2826 in 600s	2825..2854 in 600s
ta68js	2784 in 4s	2784..2810 in 600s
ta69js	3071 in 4s	3071 in 464s
ta70js	2995 in 7s	2995..3010 in 600s
ta71js	5464 in 20s	5464..5596 in 600s
ta72js	5181 in 18s	5181..5259 in 600s
ta73js	5568 in 18s	5568..5652 in 600s
ta74js	5339 in 17s	5339..5357 in 600s
ta75js	5392 in 26s	5392..5639 in 600s
ta76js	5342 in 21s	5342..5426 in 600s
ta77js	5436 in 17s	5436 in 521s
ta78js	5394 in 17s	5394..5463 in 600s
ta79js	5358 in 16s	5358..5405 in 600s
ta80js	5183 in 19s	5183..5250 in 600s

The jobshop scheduling problem benchmark library

Table of Contents

Overview of the jsplib

Classification of the jobshop instances

Similar work

Formats

Standard format

Da Col Teppan format

Taillard format

JSON format

Publications (instances)

Jobshop variants

Jobshop

No buffer jobshop (blocking jobshop)

No-wait jobshop

Cumulative jobshop

Jobshop with operators - workers

Jobshop with preemptive operators

Jobshop with arbitrary precedences

Jobshop with sequence dependent setup times

Flexible jobshop

JSPLib solutions - The State-Of-The-Art

Best known solutions - JSPLib

Fisher and Thompson (1963)

Lawrence (1984)

Adams, Balas and Zawack (1988)

Applegate and Cook (1991)

Yamada Nakano (1992)

Storer, Wu and Vaccari (1992)

Taillard (1993)

Demikol, Mehta and Uzsoy (1998)

Da Col and Teppan (2022)

DaCol and Teppan - reentrant jobshop (2022)

Publications (best known solutions)

Comparison of reference engines

ABZ instances

SWV instances

DMU instances 1-40

TA instances 1-80